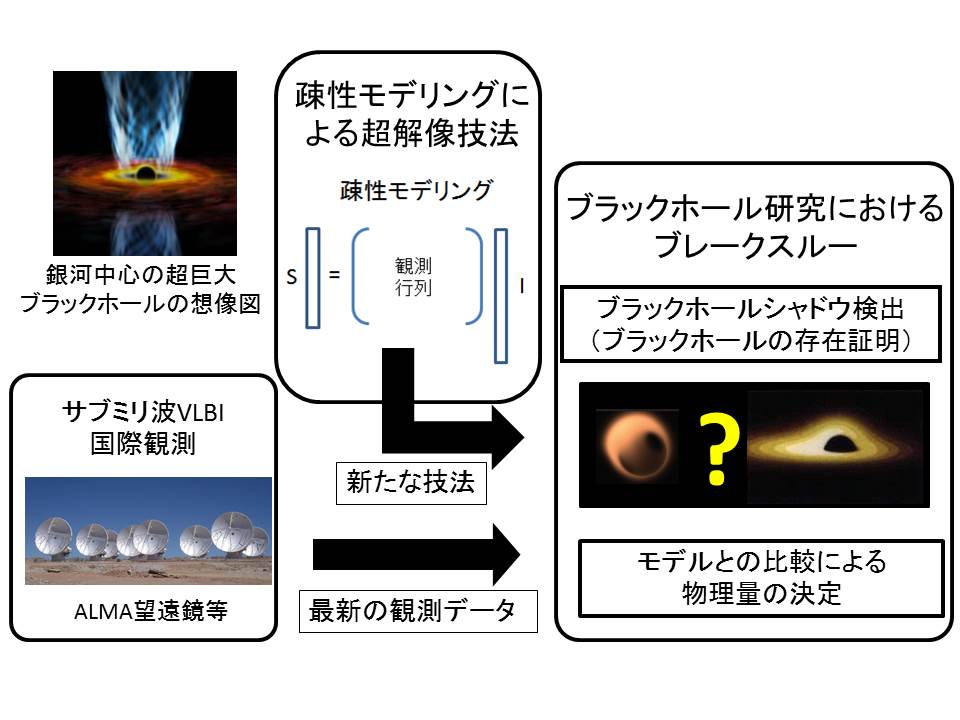
スパースモデリング

スパースモデリング（英語: Sparse modeling、スパース sparse とは「すかすか」、「少ない」を意味する）または疎性モデリングとは、少ない情報から全体像を復元しようとする科学的モデリング手法である。これは、スパース表現あるいはスパース近似という、連立一次方程式のスパース解を扱う理論に基づいている。スパースモデリング技術は、スパース解を見つけて応用するもので、画像処理、信号処理、機械学習、医用画像処理などで広く利用されている。

概要

圧縮センシングの一技法で膨大なビッグデータを解析して大量のデータに埋もれて見えにくくなってしまう有為な情報を抽出したり、法則性を導き出したり、断片的なデータを補完して実状に忠実に再現する。地球科学、MRIや天文学を含む多くの分野で高分解能化に使用される。

医用画像に関しての応用は、2002年頃に筑波大学の工藤博幸らのグループによる先駆的研究があり、2007年のカリフォルニア大学バークレー校准教授のMichael Lustigらのグループによる研究を契機として急速に広がった。

用途

スパースモデリングは、スパース表現（sparse representation）の考え方やアルゴリズムを用いて、信号処理、画像処理、機械学習、医用画像処理、配列処理、データマイニングなど、さまざまな分野で広く使用されている。

代表的な用途を次に示す。

医用画像 - MRIやX線CTでの解像度の向上
地球科学 - 地下構造の推定
天文学 - 解像度の向上
生命科学 - 核磁気共鳴分光法での計測、データ解析、立体構造計算の高速・高精度化

このように、スパース性に着想を得たモデルの使用は、幅広い用途で最先端の結果をもたらした。最近の研究では、スパース表現モデリングと深層学習の間には密接な関係があることが示唆されている。

スパース表現

上述した用途の多くでは、関心がある未知の信号は、特定の「辞書」から得たいくつかの基本要素（「アトム」という）のスパースな（疎な）組み合わせとしてモデル化され、これが問題の正則化として用いられている。これらの問題では通常、所与のデータにモデルを最もよく一致させるために辞書 $D$ を適合させることを目的とするスパース辞書学習（スパースコーディングともいう）のメカニズムが伴う。

スパース分解

ノイズのない観測

線型方程式系 $x=D\alpha$ を考える。ここで、 $D$ は劣決定 $m\times p$ 行列 ${\displaystyle (m$ であり、 $x\in \mathbb {R} ^{m},\alpha \in \mathbb {R} ^{p}$ である。ここで、行列 $D$ （通常、最大階数と仮定される）は「辞書」と呼ばれ、 $x$ は関心のある信号である。基本的なスパース表現問題は、 $x=D\alpha$ を満たす最もスパースな表現 $\alpha$ を求めることと定義される。 $D$ の列決定性により、この線形システムは一般的に無限に多くの可能な解が認められ、これらの中から非ゼロの数が最も少ないものを探す。形式的に言えば、

\min _{\alpha \in \mathbb {R} ^{p}}\|\alpha \|_{0}{\text{ subject to }}x=D\alpha

を解く。ここで $\|\alpha \|_{0}=\#\{i:\alpha _{i}\neq 0,\,i=1,\ldots ,p\}$ は $\ell _{0}$ 半ノルムで、 $\alpha$ の非ゼロ成分の数を数える。この問題は、組合せ最適化におけるNP完全な部分集合選択問題への還元を伴うNP困難であることが知られている。

$\alpha$ のスパース性とは、その中で少数の成分（ ${\displaystyle k\ll m$ ）だけが非ゼロであることを意味する。このようなスパース分解（sparse decomposition）を行う潜在的な動機は、 $x$ を $D$ のできるだけ少ない列（アトムとも呼ばれる）の線形結合として、可能な限り単純に説明したいという欲求にある。このように、信号 $x$ は、 $D$ から取り出したいくつかの基本要素（アトム）から構成される分子と見なすことができる。

上記の問題は確かにNP困難であるが、近似アルゴリズムを用いてその解を見つけることができる。そのような選択肢の一つは、 $\ell _{0}$ の代わりに $\ell _{1}$ ノルムを用いて問題を凸緩和 (en:英語版) することで得られる。ここで、 $\|\alpha \|_{1}$ は $\alpha$ 内の要素の絶対値を単純に合計したものである。これは基底追跡（basis pursuit、BP）アルゴリズムとして知られており、任意の線型計画法ソルバーを用いて処理することができる。もう一つの近似法は、マッチング追跡（matching pursuit、MP）のような貪欲法で、非ゼロの位置を一度に一つずつ見つけてゆくものである。

驚くべきことに、 $D$ に関する穏やかな条件（Spark (数学)、相互コヒーレンスまたは制限付等長性）と、解のスパース性のレベル $k$ の下で、スパース表現問題は一意の解を持つことが示され、BPとMPはそれを完全に見つけることが保証されている。

ノイズの多い観測

多くの場合、観測された信号 $x$ はノイズを含んでいる。等式制約を緩和し、データフィッティング項に $\ell _{2}$ ノルムを課すことで、スパース分解問題は、

\min _{\alpha \in \mathbb {R} ^{p}}\|\alpha \|_{0}{\text{ subject to }}\|x-D\alpha \|_{2}^{2}\leq \epsilon ^{2}

あるいはラグランジュ形式で、

\min _{\alpha \in \mathbb {R} ^{p}}\lambda \|\alpha \|_{0} {\frac {1}{2}}\|x-D\alpha \|_{2}^{2}

となる。ここで、 $\lambda$ は $\epsilon$ を置換する。

ノイズのない場合と同様に、これらの2つの問題は一般にNP困難であるが、追跡アルゴリズムを用いて近似することができる。より具体的には、 $\ell _{0}$ を $\ell _{1}$ ノルムに変更すると、

\min _{\alpha \in \mathbb {R} ^{p}}\lambda \|\alpha \|_{1} {\frac {1}{2}}\|x-D\alpha \|_{2}^{2}

が得られ、これは基底追跡ノイズ除去として知られている。同様に、マッチング追跡も上記問題の解を近似するために使用することができ、誤差しきい値に達するまで、非ゼロの位置を1つずつ見つけていく。ここでも、BPとMPは、 $D$ の特性と解 $k$ のカーディナリティに応じて、ほぼ最適な解を導くことが理論的に保証されている。

もう一つの興味深い理論的結果は、 $D$ がユニタリ行列である場合に言及され、この仮定の下では、上述の問題（ $\ell _{0}$ または $\ell _{1}$ を持つ）は、非線形縮退の形で閉形式解を認める。

バリエーション

基本的なスパース近似問題にはいくつかのバリエーションがある。

構造化スパース：この問題の元のバージョンでは、辞書に含まれる任意のアトムを選択することができる。構造化（ブロック）スパースモデルでは、個々のアトムを選択する代わりに、アトムのグループを選択する。これらのグループは、互いに重複していたり、大きさが異なる場合がある。その目的は、このブロック構造を強制しながら、スパースになるように $x$ を表現することである。

協調的（共同）スパースコーディング：この問題の元のバージョンは、単一の信号 $x$ に対して定義されている。協調的（共同）スパースコーディングモデルでは、信号の集合が利用可能であり、それぞれが $D$ からの（ほぼ）同じアトムのセットから生成すると考えられている。この場合、追求タスクの目的は、データを最もよく表す一連のスパース表現を、それらが同じ（または近くの）サポートを共有するように強制しながら再現することである。

その他の構造：より広義には、スパース近似問題は、 $\alpha$ の非ゼロ位置のパターンに特定の望ましい構造を強制しながら計算することができる。広く研究されている興味深い2つの事例は、ツリーベースの構造と、より一般的にはボルツマン分布サポートである。

アルゴリズム

上述のように、スパース表現問題

\min _{\alpha \in \mathbb {R} ^{p}}\|\alpha \|_{0}{\text{ subject to }}\|x-D\alpha \|_{2}^{2}\leq \epsilon ^{2}.

を解くために開発されたさまざまな近似（追跡（pursuit）ともいう）アルゴリズムがある。

これらの主な手法のいくつかを以下に示す。

マッチング追跡は、上記の問題を近似的に解くための貪欲反復アルゴリズムである。これは、 $\alpha$ 内の非ゼロの位置を一度に1つずつ徐々に見つけてゆく方法である。基本的な考え方は、各ステップで、現在の残余（ $x$ に初期化）と最も相関のある $D$ の列（アトム）を見つけ、新しいアトムとその係数を考慮に入れて残余を更新することである。マッチング追跡では、同じアトムが複数回選択される場合がある。
直交マッチング追跡は、マッチング追跡と非常によく似ているて、大きな違いが一つある。アルゴリズムの各ステップで、すべての非ゼロ係数が最小二乗法によって更新される。その結果、残余はすでに選択されたアトムと直交しているため、1つのアトムを複数回選択することはできない。
段階的貪欲法：上記のアルゴリズムに改良を加えたバージョンが、貪欲に動作するアルゴリズムで、2つの重要な機能が追加されている。(i) 一度に非ゼロのグループを追加する機能（ラウンドごとに1つの非ゼロではなく）と、(ii) 各ラウンドでいくつかのアトムをサポートから刈り込むプルーニングステップを含める。このアプローチの代表的なものに、部分空間追跡アルゴリズムとCoSaMPがある。
基底追跡法は、 $\ell _{0}$ を $\ell _{1}$ ノルムに置き換えることで、問題の凸緩和版を解く。これは新しい目的を定義するだけであり、望ましい解を得るためにどのようなアルゴリズムを使用するかという問題は残されていることに注意すること。このようなアルゴリズムとして一般的に考えられているのは、IRLS、LARS、および反復ソフトシュリンク法である。
スパース分解問題を解く方法としては、他にも、ホモトピー法、座標降下法、反復ハードしきい値法、上述の反復ソフトシュリンク法に関連する一次近接勾配法、ダンツィヒ・セレクタ（Dantzig selector）がある。

脚注

参考

岡田真人, 「ハイパフォマンスコンピューティングとスパースモデリング」『ハイパフォーマンスコンピューティングと計算科学シンポジウム論文集』 2014巻 2013年 p.23-24。
永田賢二, 田仲顕至, 「スパースモデリングとデータ駆動科学を実現する計算機アーキテクチャ」『システム／制御／情報』 61巻 4号 2017年 p.152-157, doi:10.11509/isciesci.61.4_152。
新部祐輔、吳湘筠, 渡辺一帆ほか, 「スパースモデリングを目的とした平行座標系表示の拡張」『情報処理学会第』 76 回全国大会 3 (2014)、頁8。
池田思朗, 「計測技術におけるスパースモデリングの応用について」『Medical Imaging Technology』 32巻 3号 2014年 p.176-181, 日本医用画像工学会, doi:10.11409/mit.32.176。
Irina Rish、Genady Grabarnik："Sparse Modeling: Theory, Algorithms, and Applications"、CRC Press、ISBN 978-1-43982869-4 (2014年11月17日)。
岡田真人, 23pAJ-5 スパースモデリングと物性物理学」『日本物理学会講演概要集』 2015年 70.1巻, セッションID 23pAJ-5, p.3115-3116, 日本物理学会, doi:10.11316/jpsgaiyo.70.1.0_3115。
大関真之, 「今日からできるスパースモデリング」京都大学大学院
池田思朗, 本間希樹, 植村誠, 「スパースモデリングと天文学(<特集>スパースモデリング: 情報処理の新しい流れ)」『応用数理』 25巻 1号 2015年 p.15-19, 日本応用数理学会, doi:10.11540/bjsiam.25.1_15。
田中利幸, 「圧縮センシング (特集スパースモデリングの発展: 原理から応用まで)--(全体概要と基本理論)」『電子情報通信学会誌』 99.5 (2016)、p.381-385, NAID 40020842497。

教科書

富岡亮太：「スパース性に基づく機械学習」、講談社サイエンティフィク、ISBN 978-4-06-152910-6 (2015年12月18日)。
Michael Elad 著、玉木徹訳『スパースモデリング: l1/l0ノルム最小化の基礎理論と画像処理への応用』共立出版、2016年4月。ISBN 978-4-320-12394-6。
永原正章：「スパースモデリング- 基礎から動的システムへの応用」、コロナ社、ISBN 978-4-339-03222-2（2017年10月31日）。
日高昇治：「スパースモデリングって何だ？データ構造を解き明かす先端技法」、カットシステム、ISBN 978-4-87783426-5 (2017年10月25日)。
Irina Rish、Genady Ya. Grabarnik：「スパースモデリング理論、アルゴリズム、応用」、ジャムハウス、ISBN 978-4-90676873-8（2019年12月27日)。
鈴木讓：「スパース推定100問」、共立出版(機械学習の数理100問シリーズ4)、ISBN 978-4-320-12509-4 (2021年1月30日).