階層ベイズモデル

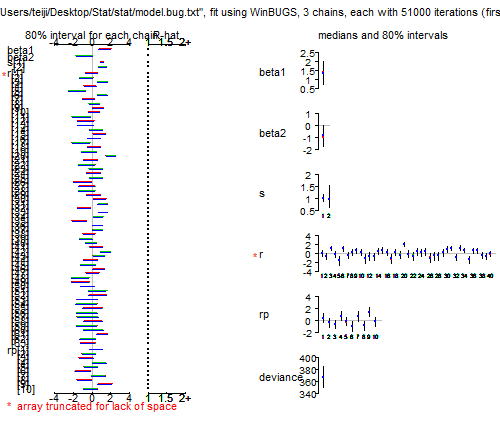
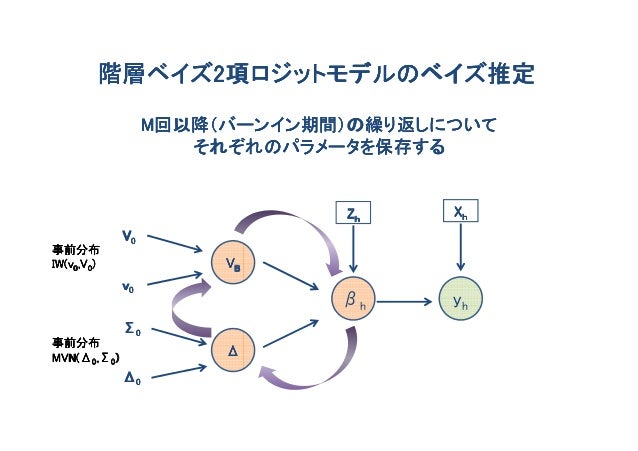
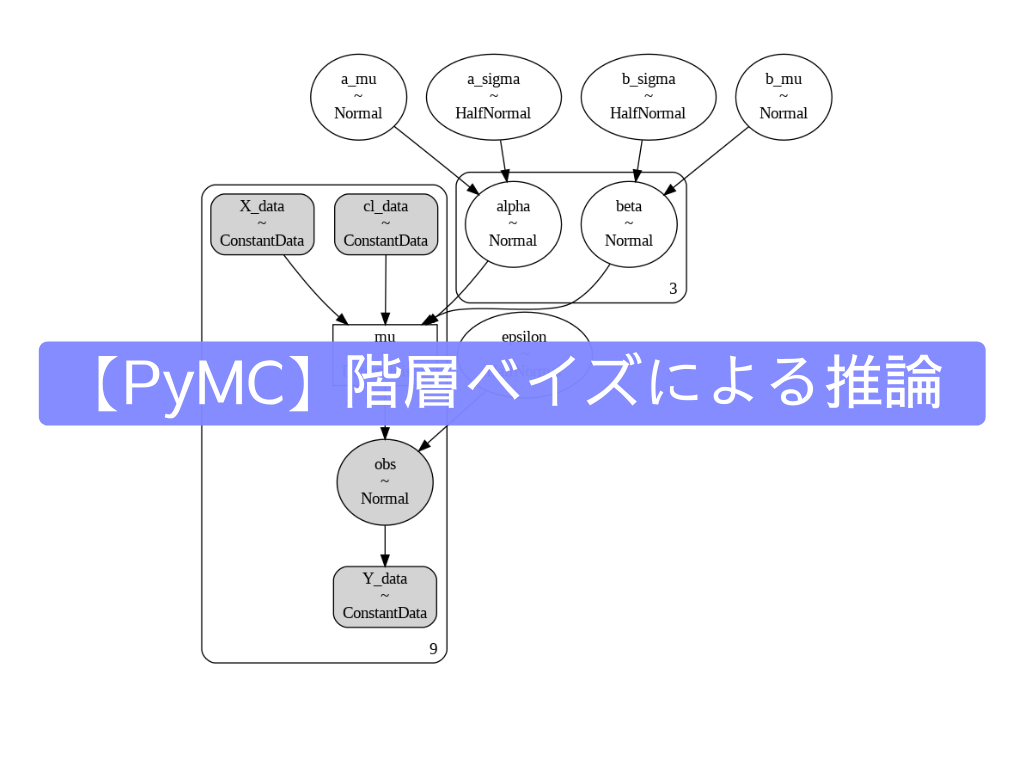
階層ベイズモデル（かいそうべいずもでる、Bayesian hierarchical modeling）は、複数のレベルで記述された、階層形式の統計モデルであり、ベイズ推定を用いて事後分布のパラメータを推定する。サブモデルを組み合わせて階層的なモデルを形成し、ベイズの定理を用いて観測データと統合して、全ての不確実性を考慮した事後分布を得る。

ベイズ統計ではパラメータを確率変数として扱い、主観的な情報に基づき、これらのパラメータの分布を仮定する。このため、頻度論的統計ではベイズ統計とは一見矛楯した結論が得られることがある。設定する問い自体が異なるため厳密に言えば矛楯するものではないが、どちらの答えを重要視するかに違いがある。ベイジアンは、意思決定と信念の更新についての関連情報を無視することはできないこと、対象者から複数の観察データが得られる場合には階層モデリングが古典的な方法を覆す可能性があることを主張する。さらに、このモデルはロバストであることが証明されており、事後分布は、より柔軟な階層的事前分布にはあまり影響されない。

階層モデリングは、複数の異なるレベルの観測単位で情報が得られる場合に使用する。例えば、複数の国の感染経路を記述する疫学モデルでは、観測単位は国であり、国毎に日々の感染者の経時的データが異なる。複数の油田やガス田の産出量の減衰曲線を説明する減衰曲線分析では、観測単位は貯蔵地域の油田またはガス田であり、それぞれに生産率経時的データがある（通常、バレル/月） 。階層モデリングのデータ構造は入れ子状である。階層的な分析・統合は、パラメータがたくさんある問題を理解するのに役立つだけでなく、計算戦略の策定にも重要な役割を果たす。

基本原理

統計的手法とモデルは、一般に、問題がこれらのパラメータの同時確率モデルの依存性を暗示するような方法で関連または接続されていると見なすことができる複数のパラメータを含む。確率の形で表される個々の信念の程度には、不確実性が伴う。その中で、時間の経過とともに信念の度合いが変化する。ホセ・M・ベルナルド教授とエイドリアン・F・スミス教授が述べたように、「学習プロセスの現実は、現実についての個人的および主観的な信念の進化にある」。これらの主観的な確率は、物理的な確率よりも精神に直接関係している。したがって、ベイジアンが特定のイベントの事前発生を考慮に入れた代替の統計モデルを策定したのは、この信念を更新する必要があるためである。

ベイズの定理

現実世界で事象が発生した場合、通常、ある選択肢における選好が修正される。これは、選択肢を定義する事象に対して個人が抱く信念の度合いを修正することで行われる。

心臓治療の効果を調べる研究で、病院 ${\displaystyle j}$ の患者の生存確率を ${\displaystyle \theta _{j}}$ とする。生存確率 ${\displaystyle \theta _{j}}$ は、心臓病患者の生存率を高めると信じる人がいる事象 ${\displaystyle y}$ の発生で更新される。

イベント ${\displaystyle y}$ が発生した状況で、${\displaystyle \theta _{j}}$ について確率の記述を更新するには、${\displaystyle \theta _{j}}$ と ${\displaystyle y}$ の同時分布 ${\displaystyle P(\theta ,\,y)}$ を与えるモデルから始めなければならない。 これは、事前分布 ${\displaystyle P(\theta )}$ とサンプリング分布 ${\displaystyle P(y\mid \theta )}$ の積として記述することができる。

${\displaystyle P(\theta ,y)=P(\theta )P(y\mid \theta )}$

条件付き確率の基本性質から、事後分布は次のようになる。

${\displaystyle P(\theta \mid y)={\frac {P(\theta ,\,y)}{P(y)}}={\frac {P(y\mid \theta )\,P(\theta )}{P(y)}}}$

この条件付き確率と個々の事象との関係を示す式をベイズの定理という。 この単純な表現の中に、更新された信念 ${\displaystyle P(\theta \mid y)}$ を適切かつ解決可能な方法で組み込むことを目的とするベイズ推定の技術的核心が含まれている。

交換可能性

統計分析は、通常、${\displaystyle n}$ 個の値 ${\displaystyle y_{1},y_{2},\ldots ,y_{n}}$ が交換可能であることを仮定することから始める。 ${\displaystyle \theta _{j}}$ を他と区別する情報がデータ ${\displaystyle y}$ しかなく、パラメータの順序付けやグループ化ができない場合、事前分布においてパラメータ間の対称性を仮定する必要がある。この対称性は、確率的には、交換可能性で表される。 一般的に、分布 ${\displaystyle P(\theta )}$ に従うパラメーターベクトル ${\displaystyle \theta }$ が与えられたとき、独立同分布としてモデル化することが有用かつ適切である。

有限の交換可能性

定数 n に対して、集合 ${\displaystyle y_{1},y_{2},\ldots ,y_{n}}$ が交換可能であるとは、同時確率 ${\displaystyle P(y_{1},y_{2},\ldots ,y_{n})}$ が添え字の順列によらず不変であることをいう。つまり、${\displaystyle 1,2,\ldots ,n}$ を並び替えて得られるすべての順列 ${\displaystyle \pi \,(\pi _{1},\pi _{2},\ldots ,\pi _{n})}$ に対して次の式が成立する。

${\displaystyle P(y_{1},y_{2},\ldots ,y_{n})=P(y_{\pi _{1}},y_{\pi _{2}},\ldots ,y_{\pi _{n}}).}$

${\displaystyle x_{1},\ldots ,x_{n}}$ が独立同分布ならば交換可能だが、交換可能であっても独立同分布であるとは限らない。 次に、交換可能だが独立同分布ではない例を示す。

壺の中に赤い玉 1 個と青い玉 1 個があり、二分の一の確率でどちらかを取り出すものとする。n 個の中から玉を 1 個取り出して、引いた玉は戻さずに、n - 1 個の中から次の玉を取り出す。

${\displaystyle Y_{i}={\begin{cases}1,&{\text{if the }}i{\text{th ball is red}},\\0,&{\text{otherwise}}.\end{cases}}}$

最初に赤い玉、2 番目に青い玉を取り出す確率も、最初に青い玉、2 番目に赤い玉を取り出す確率も、同じく二分の一であり、${\displaystyle y_{1}}$ と ${\displaystyle y_{2}}$ とは交換可能である。

${\displaystyle P(y_{1}=1,\,y_{2}=0)=P(y_{1}=0,\,y_{2}=1)={\frac {1}{2}}}$

しかし、最初に赤い玉を取り出した後で 2 番目に赤い玉を取り出す確率は 0 であり、2 回目に赤い玉を取り出す確率とは等しくない。${\displaystyle P(y_{2}=1\mid y_{1}=1)=0\neq P(y_{2}=1)={\frac {1}{2}}}$

無限の交換可能性

無限の交換可能性とは、無限数列 ${\displaystyle y_{1},y_{2},\ldots }$ のすべての有限な部分集合が交換可能である、という性質である。つまり、任意の ${\displaystyle n}$ について、数列 ${\displaystyle y_{1},y_{2},\ldots ,y_{n}}$ 交換可能である。

階層モデル

構成要素

階層ベイズモデルでは、以下の 2 つの重要な概念を利用して事後分布を導出する。

1. ハイパーパラメータ Hyperparameter：事前分布のパラメータ
2. 超事前分布 Hyper prior：ハイパーパラメータの分布

確率変数 ${\displaystyle Y}$ が、平均 ${\displaystyle \theta }$ 、分散 1 の正規分布に従うと仮定する。このことを、チルダを用いて下記のように表記する。

${\displaystyle Y\mid \theta \sim N(\theta ,1)}$

さらに、パラメータ ${\displaystyle \theta }$ が平均 ${\displaystyle \mu }$、分散 1 の正規分布に従うと仮定する。

${\displaystyle \theta \mid \mu \sim N(\mu ,1)}$

そして、ハイパーパラメータ${\displaystyle \mu }$ が標準正規分布に従うものとする。

${\displaystyle \mu \sim N(0,1)}$

このようなハイパーパラメータが従う分布を、超事前分布と呼ぶ。 ${\displaystyle Y}$ の分布の表記は、別のパラメータを追加することで変化する。

${\displaystyle Y\mid \theta ,\mu \sim N(\theta ,1)}$

ハイパーパラメータ ${\displaystyle \mu }$ が平均 ${\displaystyle \beta }$ 分散 ${\displaystyle \epsilon }$ の正規分布に従う場合、${\displaystyle \beta }$ と ${\displaystyle \epsilon }$ もまたハイパーパラメータであり、その分布も超事前分布となる。

${\displaystyle \mu \sim N(\beta ,\epsilon )}$

枠組み

${\displaystyle y_{j}}$ を観測値、${\displaystyle \theta _{j}}$ を ${\displaystyle y_{j}}$ のデータ生成過程を支配するパラメータとする。 さらに、パラメータ ${\displaystyle \theta _{1},\theta _{2},\ldots ,\theta _{j}}$ が交換可能な形で共通母集団から生成され、その分布がハイパーパラメータ ${\displaystyle \phi }$ によって規定されるものとする。 階層ベイズモデルには、次の段階が含まれる。

Stage I

${\displaystyle y_{j}\mid \theta _{j},\phi \sim P(y_{j}\mid \theta _{j},\,\phi )}$

Stage II

${\displaystyle \theta _{j}\mid \phi \sim P(\theta _{j}\mid \phi )}$

Stage III

${\displaystyle \phi \sim P(\phi )}$

尤度 ${\displaystyle P(y_{j}\mid \theta _{j},\phi )}$ は ${\displaystyle \theta _{j},\phi }$ に依存するが、${\displaystyle \phi }$ は ${\displaystyle \theta _{j}}$ を通してのみ尤度に影響する。

条件付き確率の定義から、${\displaystyle \theta _{j},\phi }$ の事前分布 ${\displaystyle P(\theta _{j},\phi )}$ は、超事前分布 ${\displaystyle P(\phi )}$ を用いて、次のように分解できる。

${\displaystyle P(\theta _{j},\,\phi )=P(\theta _{j}\mid \phi )\,P(\phi )}$

ベイズの定理から、${\displaystyle \theta _{j},\phi }$ の事後分布　${\displaystyle P(\phi ,\,\theta _{j}\mid y)}$ は次のように比例する。

${\displaystyle P(\phi ,\,\theta _{j}\mid y)\propto P(y_{j}\mid \theta _{j},\,\phi )\,P(\theta _{j},\,\phi )}$

以上から、

${\displaystyle P(\phi ,\,\theta _{j}\mid y)\propto P(y_{j}\mid \theta _{j})\,P(\theta _{j}\mid \phi )\,P(\phi )}$

例

このことをさらに説明するために、次のような例を考えてみる。ある教師が、生徒の SAT での成績を推定したいものとする。教師は、生徒の高校の成績と現在の GPA（評点平均）に関する情報を使って、推定値を算出する。生徒の現在の GPA を ${\displaystyle Y}$、SAT の成績を ${\displaystyle \theta }$ として、次のように表される。

${\displaystyle Y\mid \theta \sim P(Y\mid \theta )}$

SAT の成績は、学年 ${\displaystyle \phi }$ でインデックスされた共通の母集団分布からのサンプルとみなされる。

${\displaystyle \theta \mid \phi \sim P(\theta \mid \phi )}$

さらに、ハイパーパラメータ${\displaystyle \phi }$ は超事前分布 ${\displaystyle P(\phi )}$ が与える分布に従う。 GPAに関する情報に基づいて SAT を予測するには、

${\displaystyle P(\theta ,\,\phi \mid Y)\propto P(Y\mid \theta ,\,\phi )\,P(\theta ,\,\phi )}$

${\displaystyle P(\theta ,\,\phi \mid Y)\propto P(Y\mid \theta )\,P(\theta \mid \phi )\,P(\phi )}$

問題のすべての情報が事後分布を解くために使用される。 事前分布と尤度関数だけを使って解くのではなく、超事前分布を使うことで、より多くの情報を得て、パラメータの振る舞いについてより正確な信念を持つことができる。

2段階の階層モデル

一般に、2段階の階層モデルで関心のある共同事後分布は次の通り。

${\displaystyle P(\theta ,\phi \mid Y)={P(Y\mid \theta ,\phi )P(\theta ,\phi ) \over P(Y)}={P(Y\mid \theta )P(\theta \mid \phi )P(\phi ) \over P(Y)}}$

${\displaystyle P(\theta ,\,\phi \mid Y)\propto P(Y\mid \theta )\,P(\theta \mid \phi )\,P(\phi )}$

3段階の階層モデル

3段階の階層モデルの場合、事後分布は次の式で与えられる。

${\displaystyle P(\theta ,\,\phi ,\,X\mid Y)={\frac {P(Y\mid \theta )\,P(\theta \mid \phi )\,P(\phi \mid X)\,P(X)}{P(Y)}}}$

${\displaystyle P(\theta ,\,\phi ,\,X\mid Y)\propto P(Y\mid \theta )\,P(\theta \mid \phi )\,P(\phi \mid X)\,P(X)}$

脚注

出典

参考文献

• 久保拓弥『データ解析のための統計モデリング入門』岩波書店、2012年5月18日。ISBN 9784000069731。 

関連項目

• 一般化線形混合モデル